Cálculo del c.m. de un sistemaDistribución discreta de materia
Distribución cuasidiscreta de materia
Distribución continua de materia
Distribución cuasidiscreta de materia
Distribución continua de materia
- Distribución de masa homogénea: Si la masa está distribuida homogéneamente, la densidad será constante por lo que se puede sacar fuera de la integral haciendo uso de la relación siguiente:

- Distribución de masa no homogénea: Los centros de masas en cuerpos de densidad variable pueden calcularse si se conoce la función de densidad
 . En este caso se calcula el centro de masas de la siguiente forma.
. En este caso se calcula el centro de masas de la siguiente forma.
- Los vectores de campo en cualquier punto son siempre tangenciales a la línea de fuerza que pasa por el punto dado.
- Las líneas de fuerza no se cruzan en ningún punto aunque pueden seguir trayectorias cerradas
 .
.
- La cantidad de líneas de fuerza en cualquier porción del espacio en que se encuentra definido el campo es proporcional a la intensidad del campo vectorial.
Integral de línea
- el cálculo de la longitud de una curva en el espacio,
- o también para el cálculo del trabajo que se realiza para mover algún objeto a lo largo de una trayectoria teniendo en cuenta campos de fuerzas (descritos por campos vectoriales) que actúen sobre el mismo.
Integral curvilínea de un campo escalar
Integral curvilínea de un campo vectorial[editar]

donde
 es el producto escalar y r: [a, b] → C es una parametrización biyectiva arbitraria de la curva C de tal manera que r(a) y r(b) son los puntos finales de C.
es el producto escalar y r: [a, b] → C es una parametrización biyectiva arbitraria de la curva C de tal manera que r(a) y r(b) son los puntos finales de C.
Propiedades de un campo vectorial
Circulación y Rotacional
Flujo y divergencia
Para un sistema de masas discreto, formado por un conjunto de masas puntuales, el centro de masas se puede calcular como:

 , masa total del sistema de partículas.
, masa total del sistema de partículas.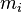 , masa de la partícula i-ésima.
, masa de la partícula i-ésima. , vector de posición de la masa i-ésima respecto al sistema de referencia supuesto.
, vector de posición de la masa i-ésima respecto al sistema de referencia supuesto.
Un poco más explícito si A1,... An son n puntos, y m1,... mn n números (m como masa). Entonces el centro de masa de los (Ai, mi) es el punto G definido como sigue:

Esta definición no depende del punto O, que puede ser cualquiera. Si se toma el origen del plano o del espacio, se obtienen las coordenadas del baricentro como promedio ponderado por los mi de las coordenadas de los puntos Ai:

La definición anterior equivale a la fórmula siguiente, más práctica para el cálculo vectorial, pues prescinde de las fracciones (se obtiene tomando O = G):


 , masa total del sistema de partículas.
, masa total del sistema de partículas.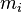 , masa de la partícula i-ésima.
, masa de la partícula i-ésima. , vector de posición de la masa i-ésima respecto al sistema de referencia supuesto.
, vector de posición de la masa i-ésima respecto al sistema de referencia supuesto.


En el caso de un sistema de cuerpos cuasipuntuales, o cuerpos que distan entre sí mucho más que las dimensiones de cada uno de los cuerpos, el cálculo anterior resulta bastante aproximado.
Para sistemas de masas continuos o distribuciones continuas de materia debemos recurrir al Cálculo Infinitesimal e Integral, de modo que la expresión anterior se escribe en la forma:


siendo V el volumen total.
Para cuerpos bidimensionales (superficies) o monodimensionales (líneas) se trabajará con densidades superficiales y longitudinales respectivamente.
Para el caso de cuerpos con densidad uniforme, el c.m. coincidirá con el centroide del cuerpo.

Definición de campo vectorial
Físicamente un campo vectorial representa la distribución espacial de una magnitud vectorial.
Matemáticamente se define un campo vectorial como una función vectorial de las coordenadas o como un caso especial de una transformación no necesariamente lineal.  , en donde
, en donde  representa el espacio vectorial que hace las veces de dominio y
representa el espacio vectorial que hace las veces de dominio y  el espacio vectorial que actúa como rango.
el espacio vectorial que actúa como rango.
 El campo ilustrado en la ecuación anterior es un campo vectorial
El campo ilustrado en la ecuación anterior es un campo vectorial  , dado que la función vectorial tiene tres componentes y cada componente es una función de tres variables independientes.
Cuando se modela la distribución de esfuerzos en una estructura, la distribución de fuerzas de naturaleza electromagnética o gravitatoria en el espacio, se hace usando campos vectoriales.
Otros ejemplos de campos vectoriales son las funciones de velocidad asociadas a las trayectorias de las partículas o diferenciales de volumen de una sustancia en condiciones de flujo bien sea laminar o turbulento.
El gradiente de un campo escalar, constituye un ejemplo adicional de campo vectorial, dado que la magnitud y dirección del gradiente de un campo escalar es una función de las coordenadas, tal como se ilustró en la Figura 19.
, dado que la función vectorial tiene tres componentes y cada componente es una función de tres variables independientes.
Cuando se modela la distribución de esfuerzos en una estructura, la distribución de fuerzas de naturaleza electromagnética o gravitatoria en el espacio, se hace usando campos vectoriales.
Otros ejemplos de campos vectoriales son las funciones de velocidad asociadas a las trayectorias de las partículas o diferenciales de volumen de una sustancia en condiciones de flujo bien sea laminar o turbulento.
El gradiente de un campo escalar, constituye un ejemplo adicional de campo vectorial, dado que la magnitud y dirección del gradiente de un campo escalar es una función de las coordenadas, tal como se ilustró en la Figura 19.

Representación de un campo vectorial
Líneas de fuerza
La representación de los campos vectoriales se hace mediante mapas semejantes a los de los campos escalares, pero usando líneas que representan la continuidad de la orientación de los vectores de campo sobre una región definida. Estas líneas reciben el nombre de líneas de fuerza.
Al igual que con los campos escalares, un campo vectorial no puede representarse fácilmente en tres dimensiones, por lo que normalmente se hacen proyecciones sobre los planos directores del sistema de coordenadas.
 Figura 20 Representación de un campo vectorial de
Figura 20 Representación de un campo vectorial de  .
.
Las líneas de fuerza cumplen con las siguientes propiedades:
En algunas otras ocasiones, la representación de campos vectoriales se hace a través de los vectores de campo directamente. En estos casos, la intensidad del campo vectorial se asocia a la densidad de vectores de campo en una región, tanto como a la longitud de los mismos.
Trazado de las líneas de fuerza de un campo vectorial
De acuerdo con la definición de línea de fuerza, una línea de fuerza es tangente a los vectores de campo en todos los puntos del espacio vectorial definido. Esto, se ilustra gráficamente en la Figura 21 .
 Figura 21 Relación entre los vectores de campo y la recta tangente a la curva en una línea de fuerza.
Se observa claramente que el vector de campo tiene la misma dirección de la recta tangente a la línea de fuerza en el punto de tangencia.
En este caso, el vector de campo tiene dos componentes denominados
Figura 21 Relación entre los vectores de campo y la recta tangente a la curva en una línea de fuerza.
Se observa claramente que el vector de campo tiene la misma dirección de la recta tangente a la línea de fuerza en el punto de tangencia.
En este caso, el vector de campo tiene dos componentes denominados  y
y  respectivamente; resulta entonces que la relación entre las componentes del vector da como resultado la pendiente de la recta tangente a la línea de fuerza en cada punto de tangencia.
Dado que la pendiente de la recta tangente es la derivada de la curva, se puede entonces proponer una igualdad definida por:
respectivamente; resulta entonces que la relación entre las componentes del vector da como resultado la pendiente de la recta tangente a la línea de fuerza en cada punto de tangencia.
Dado que la pendiente de la recta tangente es la derivada de la curva, se puede entonces proponer una igualdad definida por:
 La familia de soluciones a esta ecuación diferencial es entonces la misma familia de curvas que representa las líneas de fuerza.
Para el caso considerado en el Ejemplo 18 , el campo vectorial tiene por ecuación:
La familia de soluciones a esta ecuación diferencial es entonces la misma familia de curvas que representa las líneas de fuerza.
Para el caso considerado en el Ejemplo 18 , el campo vectorial tiene por ecuación:
 En este caso, la ecuación diferencial planteada quedaría:
En este caso, la ecuación diferencial planteada quedaría:
 La familia de soluciones de esta ecuación es de la forma:
La familia de soluciones de esta ecuación es de la forma:
 Para diferentes valores de k tanto negativos como positivos se obtienen diferentes líneas de fuerza según se ilustra en la Figura 22 .
Para diferentes valores de k tanto negativos como positivos se obtienen diferentes líneas de fuerza según se ilustra en la Figura 22 .
 Figura 22 Trazado de las líneas de fuerza del campo vectorial del Ejemplo 18 .
Figura 22 Trazado de las líneas de fuerza del campo vectorial del Ejemplo 18 .
Finalmente, la dirección de las líneas de fuerza la define la ecuación del campo vectorial, por ejemplo en el primer cuadrante, tanto x como y tienen signo positivo, por lo cual las líneas de fuerza van en la dirección del semieje x positivo y del semieje y negativo.
El mismo método de análisis se usa para definir la dirección en los cuatro cuadrantes.
Como se observa al comparar las gráficas de las líneas de fuerza y las obtenidas en el Ejemplo 17 , las líneas de fuerza son perpendiculares a las equipotenciales, como es de esperarse de acuerdo con las propiedades del vector gradiente.



Definición de campo vectorial









Físicamente un campo vectorial representa la distribución espacial de una magnitud vectorial.
Matemáticamente se define un campo vectorial como una función vectorial de las coordenadas o como un caso especial de una transformación no necesariamente lineal.  , en donde
, en donde  representa el espacio vectorial que hace las veces de dominio y
representa el espacio vectorial que hace las veces de dominio y  el espacio vectorial que actúa como rango.
el espacio vectorial que actúa como rango.
El campo ilustrado en la ecuación anterior es un campo vectorial  , dado que la función vectorial tiene tres componentes y cada componente es una función de tres variables independientes.
, dado que la función vectorial tiene tres componentes y cada componente es una función de tres variables independientes.
Cuando se modela la distribución de esfuerzos en una estructura, la distribución de fuerzas de naturaleza electromagnética o gravitatoria en el espacio, se hace usando campos vectoriales.
Otros ejemplos de campos vectoriales son las funciones de velocidad asociadas a las trayectorias de las partículas o diferenciales de volumen de una sustancia en condiciones de flujo bien sea laminar o turbulento.
El gradiente de un campo escalar, constituye un ejemplo adicional de campo vectorial, dado que la magnitud y dirección del gradiente de un campo escalar es una función de las coordenadas, tal como se ilustró en la Figura 19.

Representación de un campo vectorial
Líneas de fuerza
La representación de los campos vectoriales se hace mediante mapas semejantes a los de los campos escalares, pero usando líneas que representan la continuidad de la orientación de los vectores de campo sobre una región definida. Estas líneas reciben el nombre de líneas de fuerza.
Al igual que con los campos escalares, un campo vectorial no puede representarse fácilmente en tres dimensiones, por lo que normalmente se hacen proyecciones sobre los planos directores del sistema de coordenadas.

Figura 20 Representación de un campo vectorial de  .
.
Las líneas de fuerza cumplen con las siguientes propiedades:
En algunas otras ocasiones, la representación de campos vectoriales se hace a través de los vectores de campo directamente. En estos casos, la intensidad del campo vectorial se asocia a la densidad de vectores de campo en una región, tanto como a la longitud de los mismos.
Trazado de las líneas de fuerza de un campo vectorial
De acuerdo con la definición de línea de fuerza, una línea de fuerza es tangente a los vectores de campo en todos los puntos del espacio vectorial definido. Esto, se ilustra gráficamente en la Figura 21 .

Figura 21 Relación entre los vectores de campo y la recta tangente a la curva en una línea de fuerza.
Se observa claramente que el vector de campo tiene la misma dirección de la recta tangente a la línea de fuerza en el punto de tangencia.
En este caso, el vector de campo tiene dos componentes denominados  y
y  respectivamente; resulta entonces que la relación entre las componentes del vector da como resultado la pendiente de la recta tangente a la línea de fuerza en cada punto de tangencia.
respectivamente; resulta entonces que la relación entre las componentes del vector da como resultado la pendiente de la recta tangente a la línea de fuerza en cada punto de tangencia.
Dado que la pendiente de la recta tangente es la derivada de la curva, se puede entonces proponer una igualdad definida por:
La familia de soluciones a esta ecuación diferencial es entonces la misma familia de curvas que representa las líneas de fuerza.
Para el caso considerado en el Ejemplo 18 , el campo vectorial tiene por ecuación:
En este caso, la ecuación diferencial planteada quedaría:
La familia de soluciones de esta ecuación es de la forma:
Para diferentes valores de k tanto negativos como positivos se obtienen diferentes líneas de fuerza según se ilustra en la Figura 22 .

Figura 22 Trazado de las líneas de fuerza del campo vectorial del Ejemplo 18 .
Finalmente, la dirección de las líneas de fuerza la define la ecuación del campo vectorial, por ejemplo en el primer cuadrante, tanto x como y tienen signo positivo, por lo cual las líneas de fuerza van en la dirección del semieje x positivo y del semieje y negativo.
El mismo método de análisis se usa para definir la dirección en los cuatro cuadrantes.
Como se observa al comparar las gráficas de las líneas de fuerza y las obtenidas en el Ejemplo 17 , las líneas de fuerza son perpendiculares a las equipotenciales, como es de esperarse de acuerdo con las propiedades del vector gradiente.
Cuando las líneas de fuerza en cualquier región del espacio donde se encuentre definido el campo siguen una trayectoria cerrada se dice que el campo posee circulación en dicha región.
La circulación es una característica de los campos vectoriales y tiene una definición matemática relativamente simple.
La circulación de un campo es la sumatoria sobre una trayectoria cerrada de las componentes de campo tangenciales la trayectoria.
 Figura 23 Líneas de fuerza de un campo vectorial con circulación.
Cuando se desea medir la circulación de un campo vectorial como una función de las coordenadas, se utiliza una función vectorial denominada rotacional, que mide la circulación por unidad de área cuando el área tiende a cero en cada punto del espacio en que se encuentra definido el campo.
Figura 23 Líneas de fuerza de un campo vectorial con circulación.
Cuando se desea medir la circulación de un campo vectorial como una función de las coordenadas, se utiliza una función vectorial denominada rotacional, que mide la circulación por unidad de área cuando el área tiende a cero en cada punto del espacio en que se encuentra definido el campo.
 Donde C es la curva que encierra la superficie
Donde C es la curva que encierra la superficie  .
El rotacional de un campo es una función de las coordenadas y puede en consecuencia, ser diferente para los diferentes puntos del espacio en que se encuentra definido el campo.
Cuando el rotacional es nulo en todos los puntos de una región, se dice que el campo es irrotacional o conservativo en dicha región.
En coordenadas generalizadas el operador vectorial diferencial del rotacional es el que se muestra en la Ecuación 24.
.
El rotacional de un campo es una función de las coordenadas y puede en consecuencia, ser diferente para los diferentes puntos del espacio en que se encuentra definido el campo.
Cuando el rotacional es nulo en todos los puntos de una región, se dice que el campo es irrotacional o conservativo en dicha región.
En coordenadas generalizadas el operador vectorial diferencial del rotacional es el que se muestra en la Ecuación 24.
 Ecuación 24 Rotacional en coordenadas generalizadas.
El rotacional en los demás sistemas de coordenadas se puede obtener a partir del desarrollo de la Ecuación 24 y se encuentra en la sección de anexos.
Ecuación 24 Rotacional en coordenadas generalizadas.
El rotacional en los demás sistemas de coordenadas se puede obtener a partir del desarrollo de la Ecuación 24 y se encuentra en la sección de anexos.
Teorema de Stokes
A partir de la definición de rotacional, se deduce una identidad conocida como el teorema de Stokes:
Dado que el rotacional de un campo vectorial es una especia de derivada areolar de la circulación del campo, es lógico pensar que la integral de área del rotacional corresponda a la circulación de campo, de donde se desprende la Ecuación 25.
 Ecuación 25 Teorema de Stokes
La circulación de un campo vectorial a lo largo de cualquier trayectoria es igual al flujo del campo sobre cualquier superficie encerrada por dicha trayectoria.
Ecuación 25 Teorema de Stokes
La circulación de un campo vectorial a lo largo de cualquier trayectoria es igual al flujo del campo sobre cualquier superficie encerrada por dicha trayectoria.

Cuando las líneas de fuerza en cualquier región del espacio donde se encuentre definido el campo siguen una trayectoria cerrada se dice que el campo posee circulación en dicha región.
La circulación es una característica de los campos vectoriales y tiene una definición matemática relativamente simple.
La circulación de un campo es la sumatoria sobre una trayectoria cerrada de las componentes de campo tangenciales la trayectoria.

Figura 23 Líneas de fuerza de un campo vectorial con circulación.
Cuando se desea medir la circulación de un campo vectorial como una función de las coordenadas, se utiliza una función vectorial denominada rotacional, que mide la circulación por unidad de área cuando el área tiende a cero en cada punto del espacio en que se encuentra definido el campo.
Donde C es la curva que encierra la superficie  .
.
El rotacional de un campo es una función de las coordenadas y puede en consecuencia, ser diferente para los diferentes puntos del espacio en que se encuentra definido el campo.
Cuando el rotacional es nulo en todos los puntos de una región, se dice que el campo es irrotacional o conservativo en dicha región.
En coordenadas generalizadas el operador vectorial diferencial del rotacional es el que se muestra en la Ecuación 24.

Ecuación 24 Rotacional en coordenadas generalizadas.
El rotacional en los demás sistemas de coordenadas se puede obtener a partir del desarrollo de la Ecuación 24 y se encuentra en la sección de anexos.
Teorema de Stokes
A partir de la definición de rotacional, se deduce una identidad conocida como el teorema de Stokes:
Dado que el rotacional de un campo vectorial es una especia de derivada areolar de la circulación del campo, es lógico pensar que la integral de área del rotacional corresponda a la circulación de campo, de donde se desprende la Ecuación 25.
Ecuación 25 Teorema de Stokes
La circulación de un campo vectorial a lo largo de cualquier trayectoria es igual al flujo del campo sobre cualquier superficie encerrada por dicha trayectoria.

El flujo de un campo vectorial A se define como la cantidad de líneas de fuerza que atraviesa la superficie y es una cantidad escalar. Para cuantificarlo, se toma solamente la componente normal de las líneas que inciden sobre la superficie.
La componente normal se obtiene como la proyección del vector de campo sobre un vector unitario perpendicular a la superficie, el cual fue definido en el capítulo anterior.
 Figura 24 Flujo de un campo vectorial A a través de una superficie
Figura 24 Flujo de un campo vectorial A a través de una superficie 
 Para las superficies cerradas se define también el flujo de salida como el flujo que atraviesa la superficie cuando el vector de superficie apunta siempre hacia fuera de la superficie cerrada
Para las superficies cerradas se define también el flujo de salida como el flujo que atraviesa la superficie cuando el vector de superficie apunta siempre hacia fuera de la superficie cerrada .
.
 Figura 25 Flujo de salida de una superficie cerrada en presencia de una fuente, un sumidero o ninguno de ellos.
Cuando el flujo de salida es positivo, significa que en el interior de la superficie se encuentra una fuente de campo, es decir, que el número de líneas de fuerza que abandona la superficie es superior al número de líneas de fuerza que ingresan a ella.
Cuando el flujo de salida tiene signo negativo significa que en interior de la superficie se encuentra un sumidero, es decir el caso contrario a una fuente.
En general, las líneas de fuerza nacen en las fuentes y terminan en los sumideros.
El flujo de salida por unidad de volumen encerrado puede tomarse como una medida de la presencia de fuentes o sumideros en la región delimitada por la superficie.
Se denomina Divergencia de un campo vectorial al flujo de salida por unidad de volumen cuando la unidad de volumen se hace infinitesimal.
La divergencia de un campo vectorial es un campo escalar dada la naturaleza escalar del flujo y la naturaleza puntual de la divergencia.
Figura 25 Flujo de salida de una superficie cerrada en presencia de una fuente, un sumidero o ninguno de ellos.
Cuando el flujo de salida es positivo, significa que en el interior de la superficie se encuentra una fuente de campo, es decir, que el número de líneas de fuerza que abandona la superficie es superior al número de líneas de fuerza que ingresan a ella.
Cuando el flujo de salida tiene signo negativo significa que en interior de la superficie se encuentra un sumidero, es decir el caso contrario a una fuente.
En general, las líneas de fuerza nacen en las fuentes y terminan en los sumideros.
El flujo de salida por unidad de volumen encerrado puede tomarse como una medida de la presencia de fuentes o sumideros en la región delimitada por la superficie.
Se denomina Divergencia de un campo vectorial al flujo de salida por unidad de volumen cuando la unidad de volumen se hace infinitesimal.
La divergencia de un campo vectorial es un campo escalar dada la naturaleza escalar del flujo y la naturaleza puntual de la divergencia.
 El operador divergencia en coordenadas generalizadas es:
El operador divergencia en coordenadas generalizadas es:
 Ecuación 26 Divergencia en coordenadas generalizadas
La divergencia en los demás sistemas de coordenadas se encuentra en la sección de anexos.
Ecuación 26 Divergencia en coordenadas generalizadas
La divergencia en los demás sistemas de coordenadas se encuentra en la sección de anexos.

Teorema de la divergencia
De la definición de Divergencia, se desprende una identidad conocida como el teorema de la divergencia:
Dado que la divergencia de un campo vectorial es una especie de derivada volumétrica del flujo de salida del campo, es lógico pensar que la integral de volumen de la divergencia, corresponda al flujo total de salida del campo de donde se desprende la Ecuación 27 .
 Ecuación 27 Teorema de la divergencia.
Ecuación 27 Teorema de la divergencia.
El flujo de salida de un campo vectorial a través de cualquier superficie cerrada es igual a la integral de volumen de la divergencia del campo sobre el volumen encerrado por la superficie.
Cuando se desea calcular el flujo de salida de un campo a través de una determinada superficie cerrada, se hace evidente la simplicidad introducida mediante el teorema de la divergencia, como en el siguiente ejemplo:

Fuente: http://portales.puj.edu.co/objetosdeaprendizaje/Online/OA04/Campo%20vectorial.htm
El flujo de un campo vectorial A se define como la cantidad de líneas de fuerza que atraviesa la superficie y es una cantidad escalar. Para cuantificarlo, se toma solamente la componente normal de las líneas que inciden sobre la superficie.
La componente normal se obtiene como la proyección del vector de campo sobre un vector unitario perpendicular a la superficie, el cual fue definido en el capítulo anterior.

Figura 24 Flujo de un campo vectorial A a través de una superficie 
Para las superficies cerradas se define también el flujo de salida como el flujo que atraviesa la superficie cuando el vector de superficie apunta siempre hacia fuera de la superficie cerrada .
.

Figura 25 Flujo de salida de una superficie cerrada en presencia de una fuente, un sumidero o ninguno de ellos.
Cuando el flujo de salida es positivo, significa que en el interior de la superficie se encuentra una fuente de campo, es decir, que el número de líneas de fuerza que abandona la superficie es superior al número de líneas de fuerza que ingresan a ella.
Cuando el flujo de salida tiene signo negativo significa que en interior de la superficie se encuentra un sumidero, es decir el caso contrario a una fuente.
En general, las líneas de fuerza nacen en las fuentes y terminan en los sumideros.
El flujo de salida por unidad de volumen encerrado puede tomarse como una medida de la presencia de fuentes o sumideros en la región delimitada por la superficie.
Se denomina Divergencia de un campo vectorial al flujo de salida por unidad de volumen cuando la unidad de volumen se hace infinitesimal.
La divergencia de un campo vectorial es un campo escalar dada la naturaleza escalar del flujo y la naturaleza puntual de la divergencia.
El operador divergencia en coordenadas generalizadas es:

Ecuación 26 Divergencia en coordenadas generalizadas
La divergencia en los demás sistemas de coordenadas se encuentra en la sección de anexos.

Teorema de la divergencia
De la definición de Divergencia, se desprende una identidad conocida como el teorema de la divergencia:
Dado que la divergencia de un campo vectorial es una especie de derivada volumétrica del flujo de salida del campo, es lógico pensar que la integral de volumen de la divergencia, corresponda al flujo total de salida del campo de donde se desprende la Ecuación 27 .
Ecuación 27 Teorema de la divergencia.
El flujo de salida de un campo vectorial a través de cualquier superficie cerrada es igual a la integral de volumen de la divergencia del campo sobre el volumen encerrado por la superficie.
Cuando se desea calcular el flujo de salida de un campo a través de una determinada superficie cerrada, se hace evidente la simplicidad introducida mediante el teorema de la divergencia, como en el siguiente ejemplo:

INTEGRALES DE LINEA.
INTEGRALES DE LINEA.
En matemáticas, una integral de línea o curvilínea es aquella integral cuya función es evaluada sobre una curva. En el caso de una curva cerrada en dos dimensiones o del plano complejo, se llama también integral de contorno.
Ejemplos prácticos de su utilización pueden ser:
En matemáticas, una integral de línea o curvilínea es aquella integral cuya función es evaluada sobre una curva. En el caso de una curva cerrada en dos dimensiones o del plano complejo, se llama también integral de contorno.
Ejemplos prácticos de su utilización pueden ser:
donde: r: [a, b] → C es una parametrización biyectiva arbitraria de la curva C de tal manera que r(a) y r(b) son los puntos finales de C. Las integrales de trayectoria son independientes de la parametrización r(t), porque solo depende de la longitud del arco, también son independientes de la dirección de la parametrización r(t).
donde: r: [a, b] → C es una parametrización biyectiva arbitraria de la curva C de tal manera que r(a) y r(b) son los puntos finales de C. Las integrales de trayectoria son independientes de la parametrización r(t), porque solo depende de la longitud del arco, también son independientes de la dirección de la parametrización r(t).
Para F : Rn → Rn un campo vectorial, la integral de línea sobre la curva C, parametrizada como r(t) con t  [a, b], está definida como:
Las integrales de línea de un campo vectorial son independientes de la parametrización siempre y cuando las distintas parametrizaciones mantengan el sentido del recorrido de la curva. En caso de elegirse dos parametrizaciones con sentidos de recorrido contrarios, las integrales de línea del mismo campo vectorial resultarán con iguales módulos y signos contrarios.
[a, b], está definida como:
Las integrales de línea de un campo vectorial son independientes de la parametrización siempre y cuando las distintas parametrizaciones mantengan el sentido del recorrido de la curva. En caso de elegirse dos parametrizaciones con sentidos de recorrido contrarios, las integrales de línea del mismo campo vectorial resultarán con iguales módulos y signos contrarios.
Teorema de Green
Una curva cerrada C que es frontera de una región elemental tiene dos orientaciones:
Ø la contraria al sentido de las manecillas del reloj (positiva)
Ø la del sentido de las manecillas del reloj (negativa)
Denotemos C con orientación opuesta a la de las manecillas del reloj por C+ , y con la orientación de las manecillas como C- (ver Figura 1)
 Figura 1
Figura 1
La frontera de una región y-simple se puede descomponer en sus partes inferior y superior C1 y C2 y (en su caso) segmentos verticales a la izquierda y derecha B1 y B2 . Siguiendo la Figura 2, escribimos:
C+ = C1+ + B2+ + C2- + B1-

Figura 2
Podemos hacer una descomposición semejante de la frontera de una región x-simple en trozos izquierdo y derecho, y (en su caso) segmentos horizontales superior e inferior (ver Figura 3).
 Figura 3
Figura 3
Teorema de Green:
Este teorema relaciona una integral de línea a lo largo de una curva cerrada simple en el plano con una integral doble en la región encerrada por C.
Teorema:
Sea D una región simple y sea MD su frontera descrita por una curva orientada C+. Supongamos que P : D àR y Q : D à R son de clase C1. Entonces:

El Teorema de Green también es válido para regiones que se pueden descomponer en varios trozos, cada uno de los cuales es simple. Por ejemplo si la región D es un anillo y su frontera consiste en dos curvas C = C1 + C2 con las orientaciones indicadas en la Figura 4.

Figura 4
Si se aplica el Teorema a cada una de las regiones D1, D2 , D3 y D4 y se suman los resultados, se obtiene la identidad dada por el teorema de Green para D y su frontera C. El resultado es válido porque las integrales a lo largo de las líneas interiores opuestas se cancelan entre sí
El Teorema de Green es muy útil porque relaciona una integral de línea a lo largo de la frontera de una región con una integral de área sobre el interior de la región o viceversa:
Podemos usar el teorema para obtener una fórmula para calcular el área de una región acotada por una curva cerrada simple. Esto es:
Si P(x , y) = -y Q(x , y) = x, entonces:

Ejemplo 1:
Sea a > 0. Calcular el área (ver escena 5) de la región encerrada por la hipocicliode definida por:
…. x2/3 + y2/3 = a2/3
usando la parametrización:
… x = a cos3 (t) y = a sen3 (t) para 0 # t # 2Pi
Escena 5
Solución:
Según el teorema de Green y usando las identidades trigonométricas



obtenemos:







En el ejemplo anterior hemos utilizado el Teorema de Green para calcular una integral doble utilizando una integral de línea, el ejemplo siguiente ilustra una aplicación inversa.
Ejemplo 2.-
Usar el Teorema de Green para calcular la integral de línea:

donde C es la gráfica ilustrada en la Figura 5:
 Figura 5
Figura 5
Solución:
Como P = y3 y Q = x3 + 3xy2 , se tiene:
 y
y 
Aplicando el Teorema de Green:
 =
=
 =
=
 =
=
 =
=
 =
=
 = ¼
= ¼
Fuente: http://fcm.ens.uabc.mx/~chelo/analisis%20vectorial/nucleos/capitulo5/l6-1ab.htm
Para F : Rn → Rn un campo vectorial, la integral de línea sobre la curva C, parametrizada como r(t) con t  [a, b], está definida como:
[a, b], está definida como:
 [a, b], está definida como:
[a, b], está definida como:
Las integrales de línea de un campo vectorial son independientes de la parametrización siempre y cuando las distintas parametrizaciones mantengan el sentido del recorrido de la curva. En caso de elegirse dos parametrizaciones con sentidos de recorrido contrarios, las integrales de línea del mismo campo vectorial resultarán con iguales módulos y signos contrarios.
Teorema de Green
Una curva cerrada C que es frontera de una región elemental tiene dos orientaciones:
Ø la contraria al sentido de las manecillas del reloj (positiva)
Ø la del sentido de las manecillas del reloj (negativa)
Denotemos C con orientación opuesta a la de las manecillas del reloj por C+ , y con la orientación de las manecillas como C- (ver Figura 1)

Figura 1
La frontera de una región y-simple se puede descomponer en sus partes inferior y superior C1 y C2 y (en su caso) segmentos verticales a la izquierda y derecha B1 y B2 . Siguiendo la Figura 2, escribimos:
C+ = C1+ + B2+ + C2- + B1-

Figura 2
Podemos hacer una descomposición semejante de la frontera de una región x-simple en trozos izquierdo y derecho, y (en su caso) segmentos horizontales superior e inferior (ver Figura 3).

Figura 3
Teorema de Green:
Este teorema relaciona una integral de línea a lo largo de una curva cerrada simple en el plano con una integral doble en la región encerrada por C.
Teorema:
Sea D una región simple y sea MD su frontera descrita por una curva orientada C+. Supongamos que P : D àR y Q : D à R son de clase C1. Entonces:
|
El Teorema de Green también es válido para regiones que se pueden descomponer en varios trozos, cada uno de los cuales es simple. Por ejemplo si la región D es un anillo y su frontera consiste en dos curvas C = C1 + C2 con las orientaciones indicadas en la Figura 4.

Figura 4
Si se aplica el Teorema a cada una de las regiones D1, D2 , D3 y D4 y se suman los resultados, se obtiene la identidad dada por el teorema de Green para D y su frontera C. El resultado es válido porque las integrales a lo largo de las líneas interiores opuestas se cancelan entre sí
El Teorema de Green es muy útil porque relaciona una integral de línea a lo largo de la frontera de una región con una integral de área sobre el interior de la región o viceversa:
Podemos usar el teorema para obtener una fórmula para calcular el área de una región acotada por una curva cerrada simple. Esto es:
Si P(x , y) = -y Q(x , y) = x, entonces:
Ejemplo 1:
Sea a > 0. Calcular el área (ver escena 5) de la región encerrada por la hipocicliode definida por:
…. x2/3 + y2/3 = a2/3
usando la parametrización:
… x = a cos3 (t) y = a sen3 (t) para 0 # t # 2Pi
Escena 5
Solución:
Según el teorema de Green y usando las identidades trigonométricas
obtenemos:






En el ejemplo anterior hemos utilizado el Teorema de Green para calcular una integral doble utilizando una integral de línea, el ejemplo siguiente ilustra una aplicación inversa.
Ejemplo 2.-
Usar el Teorema de Green para calcular la integral de línea:
donde C es la gráfica ilustrada en la Figura 5:

Figura 5
Solución:
Como P = y3 y Q = x3 + 3xy2 , se tiene:
Aplicando el Teorema de Green:
 =
= =
= =
= =
= = ¼
= ¼
Fuente: http://fcm.ens.uabc.mx/~chelo/analisis%20vectorial/nucleos/capitulo5/l6-1ab.htm
No hay comentarios:
Publicar un comentario